ФИЗИКА
4.1.3. Гармонический осциллятор
Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида
(4.1.21)
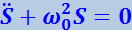 ,
,
где S – изменяющаяся величина.
Колебания гармонического осциллятора служат точкой или приближённой моделью во многих задачах классической и квантовой физики. Примерами гармонического осциллятора являются рассмотренный нами пружинный маятник, колебательный контур.
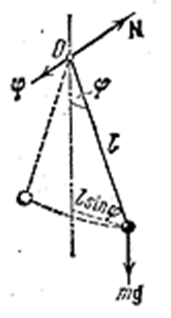
Математический маятник. Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжёлый шарик, подвешенный на длинной тонкой нити.
Отклонение маятника от положения равновесия будем характеризовать углом φ, образованным нитью с вертикалью (рис. 4.1.5). При отклонении маятника от положения равновесия возникает вращательный момент  , равный по величине mgℓ ⋅ sinφ (m – масса шарика; ℓ − длина нити). Он имеет такое направление, что стремится вернуть маятник в положение равновесия, и аналогичен в этом отношении квазиупругой силе. Поэтому так же, как смещению и квазиупругой силе, моменту
, равный по величине mgℓ ⋅ sinφ (m – масса шарика; ℓ − длина нити). Он имеет такое направление, что стремится вернуть маятник в положение равновесия, и аналогичен в этом отношении квазиупругой силе. Поэтому так же, как смещению и квазиупругой силе, моменту  и угловому смещению
и угловому смещению ![]() нужно приписывать противоположные знаки. С учётом этого, выражение для вращательного момента имеет вид:
нужно приписывать противоположные знаки. С учётом этого, выражение для вращательного момента имеет вид:
(4.1.22)
 .
.
Рис. 4.1.5 |
Напишем для маятника уравнение динамики вращательного движения. Обозначив угловое ускорение через ![]() и, учитывая, что момент инерции маятника равен mℓ2, получим:
и, учитывая, что момент инерции маятника равен mℓ2, получим:
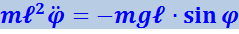
Преобразовав это уравнение, будем иметь
(4.1.23)
 .
.
Введём обозначение
(4.1.24)
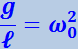
и ограничимся рассмотрением малых колебаний, когда можно положить sinφ ≈ 0, тогда придём к уравнению
(4.1.25)
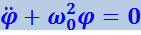 ,
,
которое идентично с уравнением (4.1.5). Его решение имеет вид
(4.1.26)
 .
.
Следовательно, при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону.
Как следует из (4.1.24) частота колебаний математического маятника не зависит от массы маятника.
По формуле (4.1.7) с учётом (4.1.24) получим:
(4.1.27)
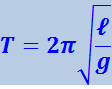 .
.
Если условие sinφ ≈ 0 не выполняется, то решив уравнение (4.1.23), можно найти для периода колебаний следующую формулу:
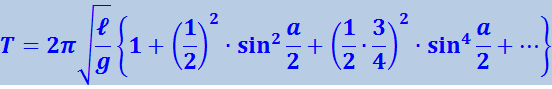 ,
,
где a – амплитуда колебаний, т.е. наибольший угол, на который отклоняется маятник из положения равновесия.
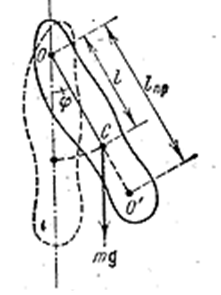
Физический маятник. Если колеблющееся тело нельзя представить как материальную точку, маятник называется физическим. При отклонении маятника от положения равновесия на угол φ возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен
(4.1.28)
 ,
,
где т – масса маятника;
ℓ − расстояние между точкой подвеса О и центром масс С маятника (рис. 4.1.6).
Знак минус имеет то же значение, что и в случае формулы (4.1.22).
Рис.4.1.6 |
Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой J, можно написать:
(4.1.29)
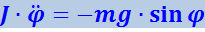 .
.
В случае малых колебаний (4.1.29) переходит в уже известное нам уравнение:
(4.1.30)
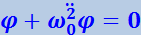 .
.
Через ω02 в данном случае обозначена величина
(4.1.31)
 .
.
Из уравнений (4.1.30) и (4.1.31) следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром масс маятника. В соответствии с (4.1.31)
(4.1.32)
 .
.
Из сопоставления (4.1.26) и (4.1.31) получается, что математический маятник с длиной
(4.1.33)

будет иметь такой период колебаний, как и данный физический маятник.
Величину (4.1.33) называют приведённой длиной физического маятника. Таким образом, приведённая длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.
Точка на прямой, соединяющей точку подвеса с центром масс, лежащая на расстоянии приведённой длины от оси вращения, называется центром качания физического маятника (точка O' на рис. 4.1.6).
Центр качания и точка подвеса обладают свойством взаимности: при переносе точки подвеса в центр качания период маятника остаётся тем же.
На этом свойстве основано определение ускорения свободного падения с помощью оборотного маятника. Оборотным маятником называется такой маятник, у которого имеются две параллельные друг другу, закреплённые вблизи его концов опорные призмы, за которые он поочерёдно подвешивается. Вдоль маятника могут перемещаться и закрепляться на нём тяжёлые грузы. Перемещением грузов добиваются того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными рёбрами призм будет равно ℓпр. Измерив период колебаний маятника и зная ℓпр, можно по формуле
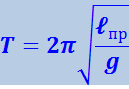
найти ускорение свободного падения g.
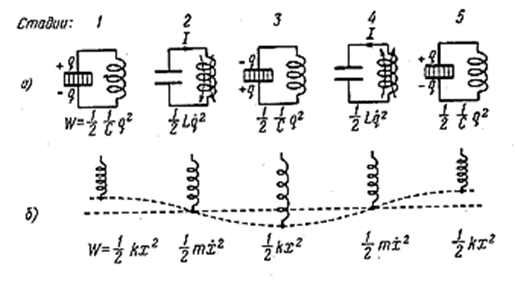
Колебательный контур. В цепи, содержащей индуктивность и ёмкость, могут возникать электрические колебания. Поэтому такая цепь называется колебательным контуром. Колебания в контуре можно вызвать, либо сообщив обкладкам конденсатора некоторый начальный заряд, либо возбудив в индуктивности ток. Воспользуемся первым способом. Последовательность стадий колебательного процесса в этом случае показана на рис. 4.1.7. Присоединим отключенный от индуктивности конденсатор к источнику напряжения. Это приведёт к возникновению на обкладках зарядов +q и -q. Между обкладками возникнет электрическое поле с энергией ![]() (стадия 1). Если затем отключить источник напряжения и замкнуть конденсатор на индуктивность, ёмкость начнёт разряжаться и в контуре потечёт ток. В результате энергия электрического поля будет уменьшаться, но зато возникнет всё возрастающая энергия магнитного поля, обусловленного током I, текущим через индуктивность. Эта энергия равна
(стадия 1). Если затем отключить источник напряжения и замкнуть конденсатор на индуктивность, ёмкость начнёт разряжаться и в контуре потечёт ток. В результате энергия электрического поля будет уменьшаться, но зато возникнет всё возрастающая энергия магнитного поля, обусловленного током I, текущим через индуктивность. Эта энергия равна ![]() .
.
Рис. 4.1.7 |
Поскольку активное сопротивление контура равно нулю, полная энергия, слагающаяся из энергий электрического и магнитного полей, не расходуется на нагревание проводов и будет оставаться постоянной. Поэтому в момент, когда напряжение на конденсаторе, а следовательно, и энергия электрического поля обращается в нуль, энергия магнитного поля, а значит, и ток достигают максимального значения (стадия 2; начиная с этого момента ток течёт за счёт э.д.с. самоиндукции). В дальнейшем ток уменьшается, и, когда заряды на обкладках достигнут первоначального значения q, сила тока станет равной нулю (стадия 3). Затем те же процессы протекают в обратном направлении (стадии 4 и 5), после чего система приходит в исходное состояние (стадия 5) и весь цикл повторяется снова и снова. В ходе процесса периодически изменяются (т.е. колеблются) заряды на обкладках, напряжение на конденсаторе и сила тока, текущего через индуктивность. Колебания сопровождаются взаимными превращениями энергий электрического и магнитного полей.
На рис. 4.1.7б колебаниям в контуре сопоставлены колебания пружинного маятника. Сообщению зарядов обкладкам конденсатора соответствует выведение маятника внешней силой из положения равновесия и сообщение ему первоначального отклонения х. При этом возникает потенциальная энергия упругой деформации пружины, равная ![]() . Стадии 2 соответствует прохождение маятника через положение равновесия. В этот момент квазиупругая сила равна нулю и маятник продолжает двигаться по инерции. К этому времени энергия маятника полностью переходит в кинетическую энергию и определяется выражением
. Стадии 2 соответствует прохождение маятника через положение равновесия. В этот момент квазиупругая сила равна нулю и маятник продолжает двигаться по инерции. К этому времени энергия маятника полностью переходит в кинетическую энергию и определяется выражением ![]() и т.д.
и т.д.
Из сопоставления электрических и механических колебаний следует, что энергия электрического поля ![]() аналогична потенциальной энергии упругой деформации, а энергия магнитного поля
аналогична потенциальной энергии упругой деформации, а энергия магнитного поля ![]() аналогична кинетической энергии. Индуктивность L играет роль массы т, величина, обратная ёмкости – роль жёсткости К. Наконец, заряду соответствует смещение маятника из положения равновесия х, а силе тока I – скорость ν. Дальше мы увидим, что аналогия между электрическими и механическими колебаниями распространяется и на описывающие их математические уравнения.
аналогична кинетической энергии. Индуктивность L играет роль массы т, величина, обратная ёмкости – роль жёсткости К. Наконец, заряду соответствует смещение маятника из положения равновесия х, а силе тока I – скорость ν. Дальше мы увидим, что аналогия между электрическими и механическими колебаниями распространяется и на описывающие их математические уравнения.
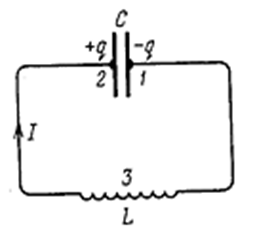
Найдём уравнение колебаний в контуре без активного сопротивления. Условимся считать положительным ток, заряжающий конденсатор (рис. 4.1.8). Тогда
(4.1.34)
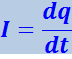 .
.
Рис. 4.1.8 |
Напишем для цепи 1-3-2 закон Ома
(4.1.35)
 .
.
В нашем случае ![]() ,
, ![]() . Подстановка этих значений в (4.1.35) даёт:
. Подстановка этих значений в (4.1.35) даёт:
(4.1.36)
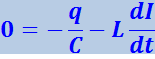 .
.
Наконец, заменив ![]() через
через ![]() , получим уравнение
, получим уравнение
(4.1.37)
 .
.
Если ввести обозначение
(4.1.38)
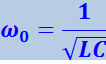
уравнение (4.1.37) принимает вид
(4.1.39)
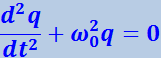 ,
,
хорошо знакомый нам из учения о механических колебаниях (4.1.5). Решением этого уравнения является функция
(4.1.40)
 .
.
Таким образом, заряд на обкладках конденсатора изменяется по гармоническому закону с частотой, определяемой выражением (4.1.38). Эта частота называется собственной частотой контура. Для периода колебаний получается формула Томсона:
(4.1.41)
 .
.
Напряжение на конденсаторе U отличается от заряда множителем 1/C:
(4.1.42)
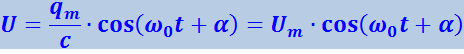 .
.
Продифференцировав функцию (4.1.40) по времени, получим выражение для силы тока
(4.1.43)
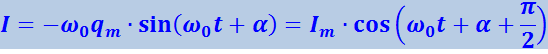 .
.
Таким образом, сила тока опережает по фазе напряжение на конденсаторе на π/2. Из формулы (4.1.42) и (4.1.43) следует, что
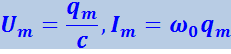 .
.
Взяв отношение этих амплитуд и, заменив ω0 по формуле (4.1.38), получим
(4.1.44)
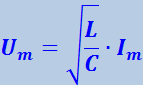 .
.
к к к