ФИЗИКА

4.1.2. Гармонические колебания

Простейшими являются гармонические колебания, т.е. такие, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Этот вид колебаний особенно важен по двум причинам: во-первых, колебания в природе и в технике часто имеют характер очень близкий к гармоническим, и во-вторых, периодические процессы иной формы могут быть представлены как наложение нескольких гармонических колебаний.

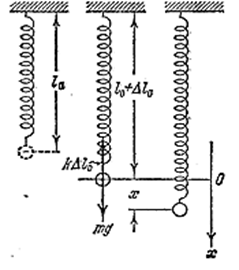
Начнём с рассмотрения механических гармонических колебаний. В качестве примера рассмотрим систему, состоящую из шарика массы т, подвешенного на пружине, массой которой можно пренебречь по сравнению с т (рис. 4.1.1). В положении равновесия сила mg уравновешивается силой k⋅Δℓ0:

(4.1.1)

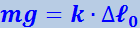
(Δℓ0 − удлинение пружины).

Будем характеризовать смещение шарика из положения равновесия координатой х, причём ось х направим по вертикали вниз, а нуль оси совместим с положением равновесия шарика. Если сместить шарик в положение, характеризуемое координатой х, то удлинение пружины станет равным Δℓ0 + х и проекция результирующей силы на ось х примет значение F = mg - k (Δℓ0 +x). Учтя (1.1), получим, что

(4.1.2)

Таким образом, в рассмотренном примере результирующая силы тяжести и упругой силы имеет характер квазиупругой силы.

Сообщим шарику смещение х = а. После чего предоставим систему самой себе. Под действием квазиупругой силы шарик будет двигаться к положению равновесия со всё возрастающей скоростью . При этом потенциальная энергия системы , будет убывать, но зато появится всё возрастающая кинетическая энергия . Придя в положение равновесия, шарик продолжает двигаться по инерции. Это движение будет замедленным и прекратится тогда, когда кинетическая энергия полностью превратится в потенциальную, т.е. смещение шарика станет равным а. Затем такой же процесс будет протекать при движении шарика в обратном направлении. Если трение в системе отсутствует, энергия системы должна сохраняться и шарик будет двигаться в пределах от х = а до х = −а неограниченно долго.

Чтобы определить характер движения запишем для шарика второй закон Ньютона:

(4.1.3)

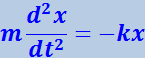
Введя обозначение

(4.1.4)

,

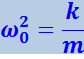преобразуем уравнение (4.1.3) следующим образом:

(4.1.5)

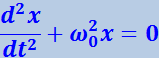
Общее решение этого уравнения имеет вид

(4.1.6)

где а и α – произвольные постоянные.

Итак, смещение х изменяется со временем по закону косинуса. Следовательно, движение системы, находящейся под действием силы вида F = -kx, представляет собой гармоническое колебание.

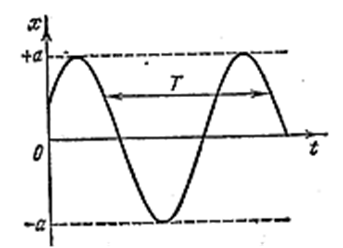
График гармонического колебания, т.е. график функции (4.1.6), показан на рис. 4.1.2.

По горизонтальной оси отложено время t, по вертикальной оси – смещение х. Поскольку косинус изменяется в пределах от -1 до +1, значения х лежат в пределах от –а до +а.

Величина небольшого отклонения системы от положения равновесия называется амплитудой колебания. Амплитуда а – постоянная положительная величина. Её значение определяется величиной первоначального отклонения.

Величина (ω0t + α), стоящая под знаком косинуса, называется фазой колебания. Постоянная α представляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебания. С изменением начала отсчёта времени изменяется и α. Следовательно, значение начальной фазы определяется выбором начала отсчёта времени. Так как значение х не изменяется при добавлении или вычитании из фазы целого числа, всегда можно добиться того, чтобы начальная фаза была по модулю меньше π. Поэтому обычно рассматриваются только значения α, лежащие в пределах от –π до +π.

Поскольку косинус – периодическая функция с периодом 2π, различные состояния системы, совершающей гармонические колебания, повторяются через такой промежуток времени Т, за который фаза колебания получает приращение, равное 2π (рис. 1.2). Этот промежуток времени Т называется периодом колебания. Он может быть определён из следующего условия:

,

откуда

(4.1.7)

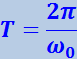
Число колебаний в единицу времени называется частотой колебания 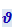. Очевидно, что частота связана с периодом соотношением:

(4.1.8)

.

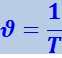За единицу частоты принята частота такого колебания, период которого равен 1 с. Эту единицу называют герцем (Гц). Частота в 103 Гц называется килогерцем (кГц), в 106 Гц – мегагерцем (МГц) и т.д.

Из (4.1.7) следует, что

(4.1.9)

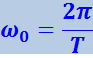
Таким образом, ω0 определяет число колебаний за 2π секунд. Величину ω0 называют круговой или циклической частотой. Она связана с обычной частотой соотношением

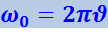
Найдём скорость и ускорение шарика.

Продифференцировав (4.1.6) по времени, получим выражение для скорости

(4.1.10)

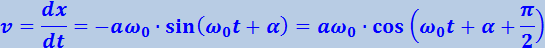
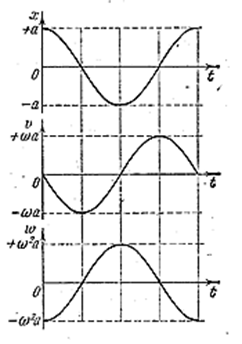
Как видно из (4.1.10) скорость также изменяется по гармоническому закону, причём амплитуда скорости равна a ω0. Из сравнения (4.1.6) и (4.1.10) следует, что скорость опережает смещение по фазе на π/2. Продифференцировав ещё раз по времени, найдём выражение для ускорения ẋ:

(4.1.11)

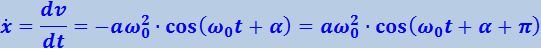
Как следует из (4.1.11), ускорение и смещение находятся в противофазе. На рис. 4.1.3 сопоставлены графики для смещения, скорости и ускорения.

Каждое конкретное колебание характеризуется определёнными значениями амплитуды a и начальной фазы α. Значения этих величин для данного колебания могут быть определены из так называемых начальных условий, т.е. по значениям отклонения х0 и ν0 в начальный момент времени. Действительно, положив в (4.1.6) и (4.1.10) t = 0, получим два уравнения:

,

из которых следует, что

(4.1.12)

,

(4.1.13)

.

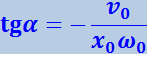Уравнение (4.1.13) удовлетворяется двумя значениями α, лежащими в интервале от -π до +π. Из этих значений нужно взять то, при котором получаются правильные знаки у косинуса и синуса.

Квазиупругая сила является консервативной. Поэтому полная энергия гармонического колебания должна оставаться постоянной. В процессе колебаний, как уже отмечено, происходит превращение кинетической энергии в потенциальную и обратно, причём в моменты наибольшего отклонения от положения равновесия полная энергия Е состоит только из потенциальной энергии, которая достигает своего наибольшего значения Epmax:

(4.1.14)

;

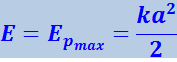при прохождении же системы через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в эти моменты достигает своего наибольшего значения Ekmax:

(4.1.15)

.

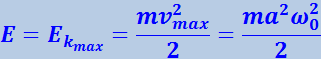Выражения (4.1.14) и (4.1.15) равны друг другу, так как согласно (4.1.4) mω02 = k. Выясним, как меняется со временем кинетическая и потенциальная энергия гармонического колебания. Кинетическая энергия равна

(4.1.16)

.

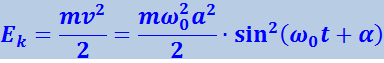Потенциальная энергия выражается формулой

(4.1.17)

.

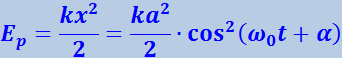Сложив (4.1.16) с (4.1.17) и приняв во внимание, что mω02 = k, получим формулу для полной энергии:

(4.1.18)

.

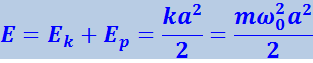Таким образом, полная энергия гармонического колебания действительно оказывается постоянной.

Выражениям для Ek и Ep, используя формулы тригонометрии, можно придать следующий вид:

(4.1.19)

;

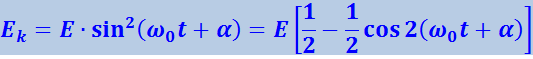(4.1.20)

,

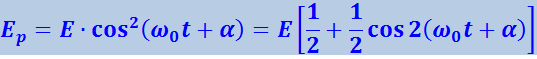где Е – полная энергия системы.

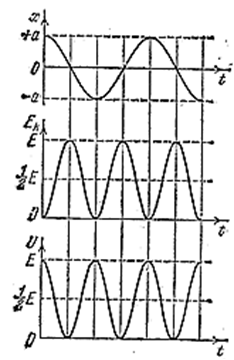
Из этих формул видно, что Ek и Ep изменяются с частотой 2ω0, т.е. с частотой в два раза превышающей частоту гармонического колебания. На рис. 4.1.4 сопоставлены графики для х, Ek и Ep.

Среднее значение квадрата синуса и квадрата косинуса равно половине. Следовательно, среднее значение Ek совпадает со средним значением Ep и равно E/2.

к к к