ФИЗИКА
1.5.5. Неинерциальные системы отсчёта
Существование инерциальных систем отсчёта постулировано в первом законе Ньютона.
Опытным путём установлено, что инерциальной можно считать гелиоцентрическую систему отсчёта. Поскольку любая другая система отсчёта, движущаяся относительно гелиоцентрической равномерно и прямолинейно, также является инерциальной, существует бесконечное множество инерциальных систем отсчёта.
До сих пор именно этими системами мы всегда пользовались для описания механического движения тел. Между тем во многих случаях необходимо изучать движение по отношению к неинерциальным системам отсчёта, т.е. к таким системам, которые движутся ускоренно относительно инерциальных.
Так, например, движение тел на Земле естественно рассматривать в лабораторной системе отсчёта, которая, как уже отмечено, строго говоря, не является инерциальной. Об этом, в частности, свидетельствует целый ряд явлений – «самопроизвольный» поворот плоскости качания маятника (опыт Фуко), отклонение свободно падающих тел к востоку, подмывание одного из берегов реками, текущими в меридиональном направлении и т.д.
Конечно, неинерциальность этой системы отсчёта не велика и в большинстве задач механики ею можно пренебречь. Однако возможность такого допущения требует специального обоснования, так как иначе неясна величина возникающих при этом погрешностей.
Отметим важную особенность неинерциальных систем отсчёта. В них скорость хода часов в различных точках различна. Поэтому не ясно, как можно измерить длительность процессов, начинающихся в одной точке и заканчивающихся в другой. Усложняется также проблема измерения и сравнения длин. Например, трудно определить понятие длины движущегося тела, если не ясно, что такое одновременность в различных точках.
Ниже мы ограничимся рассмотрением движения с малыми скоростями, когда все эти трудности не возникают и можно считать, что пространственно-временные соотношения в неинерциальной системе отсчёта являются такими же, как и в инерциальной.
С учётом этого допущения на конкретных примерах рассмотрим влияние ускорения системы отсчёта на происходящие в ней механические процессы.
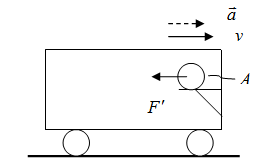
Пусть имеем вагон, который первоначально движется прямолинейно с постоянной скоростью  в направлении, указанном стрелкой на рис. 1.28.1. Пусть у передней стенки вагона на горизонтальной полке лежит шар А с массой т. Полку будем считать абсолютно скользкой, так что между ней и шаром не возникает никаких сил трения. Рассмотрим явления, происходящие внутри вагона с точки зрения двух систем отсчёта:
в направлении, указанном стрелкой на рис. 1.28.1. Пусть у передней стенки вагона на горизонтальной полке лежит шар А с массой т. Полку будем считать абсолютно скользкой, так что между ней и шаром не возникает никаких сил трения. Рассмотрим явления, происходящие внутри вагона с точки зрения двух систем отсчёта:
1) системы, связанной с полотном железной дороги;
2) системы отсчёта, связанной с вагоном.
Рис. 1.28.1 |
При прямолинейном и равномерном движениях в обеих системах на шар не действуют никакие силы (кроме уравновешивающих друг друга силы тяжести и силы реакции опоры). Предположим теперь, что вагон приобрёл постоянное ускорение 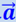 , направленное в ту же сторону, куда направлена и скорость вагона
, направленное в ту же сторону, куда направлена и скорость вагона  .
.
Рассмотрим поведение шарика А в обеих системах отсчёта. Относительно полотна шар продолжает двигаться с первоначальной скоростью  и вследствие этого отстаёт от вагона.
и вследствие этого отстаёт от вагона.
В результате, шар, ранее покоившийся относительно полки вагона, начинает скользить по ней в направлении, обратном движению вагона. Отсюда следует, что относительно системы отсчёта, связанной с вагоном, шар приобрёл ускорение 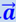 .
.
Если допустить, что в системе отсчёта, связанной с вагоном (которая не инерциальна), справедлив второй закон Ньютона, то появление в этой системе ускорения можно формально объяснить действием на шар силы
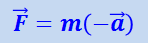 ,
,
где т – масса шара и 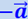 его ускорение относительно вагона, численно равное ускорению самого вагона.
его ускорение относительно вагона, численно равное ускорению самого вагона.
Эта фиктивная сила, которую приходится вводить в ускоренной системе отсчёта, чтобы в ней выполнялся второй закон Ньютона, называется инерционной силой или силой инерции.
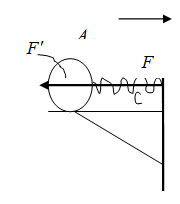
Рис. 1.28.2 |
Предположим теперь, что шар, лежащий на полке, скреплён со стенкой вагона пружиной С (рис. 1.28.2). Тогда при ускорении вагона шар будет отставать от вагона лишь до тех пор, пока пружина не растянется настолько, что появившаяся, благодаря растяжению пружины, сила не окажется достаточной, чтобы сообщить шару ускорение  , равное ускорению вагона. Другими словами: пружина тянет шар за вагоном с силой
, равное ускорению вагона. Другими словами: пружина тянет шар за вагоном с силой 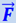 , эта сила приложена к шару, направлена в сторону ускорения вагона
, эта сила приложена к шару, направлена в сторону ускорения вагона  и численно равна
и численно равна 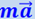 , где т – масса шара. По третьему закону Ньютона существует вторая сила
, где т – масса шара. По третьему закону Ньютона существует вторая сила  , приложенная к пружине и направленная в сторону, обратную направлению ускорения вагона.
, приложенная к пружине и направленная в сторону, обратную направлению ускорения вагона.
По отношению же к системе отсчёта, связанной с вагоном, шар, после того как пружина растянулась, снова окажется относительно вагона в состоянии покоя. Следовательно, в этой системе отсчёта, согласно второму закону Ньютона, сумма сил, приложенных к шару, должна равняться нулю. Этому требованию можно удовлетворить, если приложить к шару инерциальную силу  и считать, что она уравновешивает силу
и считать, что она уравновешивает силу 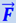 , с которой растянутая пружина тянет шар. Эта инерционная сила
, с которой растянутая пружина тянет шар. Эта инерционная сила 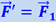 ; таким образом, силу
; таким образом, силу 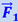 , появление которой обусловлено выполнением третьего закона Ньютона и которая приложена к пружине («связям») в ускоренной системе отсчёта, мы прилагаем к самому телу (шару А). Пользуясь ускоренной системой, связанной с вагоном, мы заменяем динамическую задачу задачей статической, задачей о равновесии шара. Для этого мы считаем приложенной к шару А не только действующую на него действительную силу
, появление которой обусловлено выполнением третьего закона Ньютона и которая приложена к пружине («связям») в ускоренной системе отсчёта, мы прилагаем к самому телу (шару А). Пользуясь ускоренной системой, связанной с вагоном, мы заменяем динамическую задачу задачей статической, задачей о равновесии шара. Для этого мы считаем приложенной к шару А не только действующую на него действительную силу 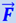 , но и силу
, но и силу 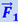 , действующую на связь. Такая замена динамической задачи статической возможна для любого случая ускоренного движения.
, действующую на связь. Такая замена динамической задачи статической возможна для любого случая ускоренного движения.
Пусть на материальную точку с массой т действует сила 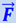 . Уравнение движения этой материальной точки выразится вторым законом Ньютона:
. Уравнение движения этой материальной точки выразится вторым законом Ньютона:
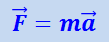
или
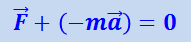 .
.
Величина 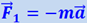 по третьему закону Ньютона представляет собой силу, действующую на те тела, которые, воздействуя на рассматриваемую материальную точку, сообщают ей ускорение. Прилагая же мысленно силу
по третьему закону Ньютона представляет собой силу, действующую на те тела, которые, воздействуя на рассматриваемую материальную точку, сообщают ей ускорение. Прилагая же мысленно силу 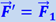 к самой материальной точке и называя её силой инерции, мы получим
к самой материальной точке и называя её силой инерции, мы получим
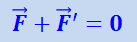 ,
,
т.е. в каждый данный момент сила инерции и сила, приложенная к материальной точке, уравновешиваются. Это положение носит название принципа Даламбера.
Рассмотрим ещё ряд примеров возникновения инерционных сил. Предположим, что на полу лифта лежит груз с массой т. Если лифт поднимается вверх с ускорением 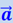 , то такое же ускорение приобретает и груз. Груз приобретает это ускорение в результате давления со стороны пола, добавочного по отношению к тому давлению, которое уравновешивает вес груза. Сила этого давления
, то такое же ускорение приобретает и груз. Груз приобретает это ускорение в результате давления со стороны пола, добавочного по отношению к тому давлению, которое уравновешивает вес груза. Сила этого давления 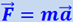 . По третьему закону Ньютона груз в свою очередь давит на пол с добавочной силой
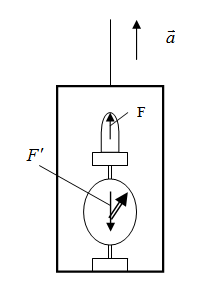
. По третьему закону Ньютона груз в свою очередь давит на пол с добавочной силой 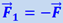 . Если груз лежит не прямо на полу, а на чашке пружинных весов (рис. 28.3), то эта сила
. Если груз лежит не прямо на полу, а на чашке пружинных весов (рис. 28.3), то эта сила 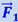 давит на весы; пружина весов сожмётся сильнее, и если весы при отсутствии ускорения лифта указывали вес груза
давит на весы; пружина весов сожмётся сильнее, и если весы при отсутствии ускорения лифта указывали вес груза 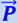 , то теперь они укажут вес
, то теперь они укажут вес 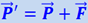 , где
, где 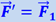 .
.
Рис. 1.28.3 |
В случае если лифт опускается с ускорением 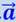 , то с таким же ускорением будет двигаться вниз вместе с лифтом и груз. Часть силы тяжести, действующей на груз, будет сообщать ему ускорение. Эта часть силы равна
, то с таким же ускорением будет двигаться вниз вместе с лифтом и груз. Часть силы тяжести, действующей на груз, будет сообщать ему ускорение. Эта часть силы равна 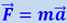 , откуда давление на весы окажется равным
, откуда давление на весы окажется равным  .
.
В обоих случаях показания весов отличны от того показания (Р), которое они дают при отсутствии ускорения у лифта.
По отношению же к системе отсчёта, связанной неизменно с лифтом, груз продолжает в обоих случаях покоиться и изменение показаний весов может быть истолковано изменением веса груза, вызванное тем, что к его истинному весу 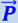 инерционная сила
инерционная сила  (направленная в ту же сторону, что и
(направленная в ту же сторону, что и 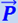 , если ускорение лифта
, если ускорение лифта 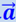 направлено вверх, и направленная в сторону, противоположную
направлено вверх, и направленная в сторону, противоположную 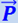 , если
, если 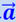 направлено вниз).
направлено вниз).
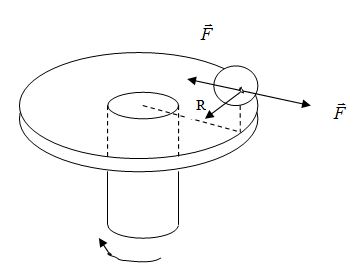
Совершенно аналогичным образом объясняется возникновение инерционных сил во вращающейся системе. Пусть сидящий на карусели человек держит в руках камень с массой т (рис. 1.28.4). Для того, чтобы камень двигался вместе с каруселью, т.е. описывал круг радиуса R (где R – расстояние от оси карусели до камня), необходимо камню сообщать центростремительное ускорение an = ω2R, где ω - угловая скорость вращения карусели. Для этого к камню должна быть приложена центростремительная сила F = m ⋅ ω2R. Человек должен непрерывно тянуть камень к себе, чтобы заставить его заворачивать. Не будь силы 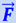 , камень начал бы двигаться по касательной τ. По третьему закону Ньютона камень действует на руки человека с силой
, камень начал бы двигаться по касательной τ. По третьему закону Ньютона камень действует на руки человека с силой 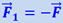 . Эта сила приложена к рукам человека и направлена от центра карусели наружу. Она называется центробежной.
. Эта сила приложена к рукам человека и направлена от центра карусели наружу. Она называется центробежной.
Рис. 1.28.4 |
Однако если рассматривать весь процесс по отношению к системе отсчёта, вращающейся вместе с диском, то камень остаётся неподвижным в этой системе отсчёта и необходимость прилагать к нему силу  может быть истолкована как результат того, что к самому камню оказалась приложена сила
может быть истолкована как результат того, что к самому камню оказалась приложена сила 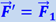 , направленная от центра карусели наружу. Это есть инерционная сила, совершенно аналогичная инерционным силам, рассмотренным нами в примерах с ускорениями вагона и лифта.
, направленная от центра карусели наружу. Это есть инерционная сила, совершенно аналогичная инерционным силам, рассмотренным нами в примерах с ускорениями вагона и лифта.
В повседневной жизни нам часто приходится встречаться с инерционными силами. Например, когда автомобиль начинает резко тормозить или поворачивать на большом ходу, мы оказываемся соответственно отброшенными, по отношению к автомобилю вперёд или в сторону, наружную по отношению к завороту; это является следствием того, что мы сохраняем скорость, которую имели раньше, автомобиль же приобретает ускорение. По отношению же к системе отсчёта, связанной с автомобилем, эти относительные смещения объясняются действием инерционных сил. Эти силы приходится учитывать во всякой ускоренной системе, как добавочные по отношению к силам, действующим в инерциальной системе.
Центробежные силы инерции используются во всех центробежных механизмах: насосах, сепараторах и т.д., где они достигают огромных значений. При проектировании быстро вращающихся деталей машин (роторов, винтов самолётов и т.д.) принимаются специальные меры для уравновешивания центробежных сил инерции.
В общей теории относительности силы инерции эквивалентны силам тяготения. В примере с лифтом мы видели, что ускорение лифта ведёт к тому же результату, как если бы груз становился тяжелее или легче (в зависимости от направления ускорения 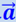 ), т.е. силы оказываются эквивалентными силами тяжести.
), т.е. силы оказываются эквивалентными силами тяжести.
Таким образом, выходит, что ускорение какой-либо системы эквивалентно появлению в этой системе сил тяготения. Однако, как показал В.А. Фок, такая эквивалентность несправедлива в пределах больших пространственных и временных масштабов.
Зависимость силы тяжести от широты местности. Пользование инерционными силами весьма удобно для решения различных механических задач в ускоренной системе, в частности, во вращающейся системе. Такого рода вращающейся системой является и земной шар. Поэтому при точном рассмотрении различных механических процессов, происходящих на поверхности Земли, следует принимать во внимание инерционные силы, возникающие от суточного вращения. Эти силы невелики, поэтому во многих случаях ими можно пренебречь.
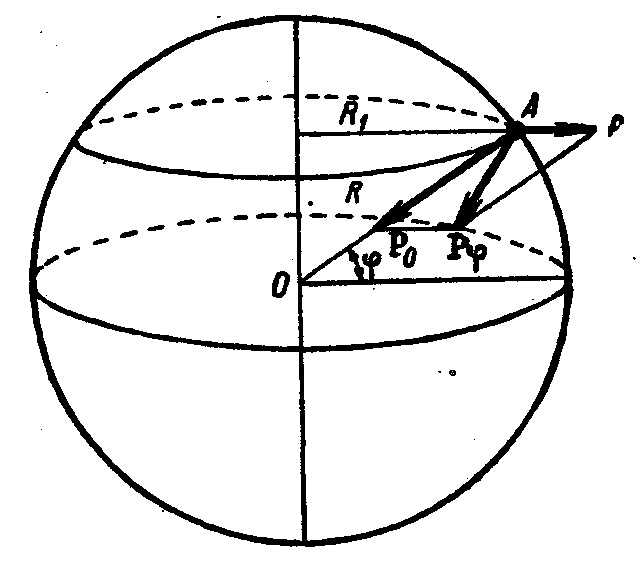
Рассмотрим влияние суточного вращения Земли на силу тяжести. Пусть тяжёлое тело А с массой т находится на широте φ (рис. 1.28.5). Решая задачу по отношению к координатной системе, вращающейся вместе с Землёй, мы должны учесть инерционную силу
(1.28.1)
 ,
,
где τ - угловая скорость вращения Земли и R1 - расстояние от земной оси до тела.
Сила 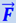 направлена перпендикулярно к земной оси. Эта сила
направлена перпендикулярно к земной оси. Эта сила 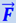 складывается с силой тяжести тела
складывается с силой тяжести тела 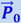 , направленной к центру Земли. С учётом этого кажущийся вес тела
, направленной к центру Земли. С учётом этого кажущийся вес тела 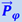 на широте φ равен
на широте φ равен
(1.28.2)
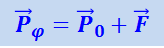 .
.
Рис. 1.28.5 |
Из рис. 1.28.5 имеем: R1 = R ⋅ cosφ , где R - радиус Земли. Тогда по (1.28.1)
(1.28.3)
 .
.
Эта сила мала по сравнению с силой тяжести. В самом деле, P0 = mg0, откуда
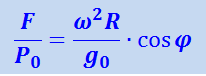 ;
;
если подставить вместо ω, R и g0 их численные значения, то окажется, что
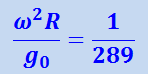 ,
,
косинус же угла φ всегда ≤1, т.е. действительно сила F много меньше силы тяжести P0.
С учётом этого, а также принимая во внимание, что Земля не представляет собой правильной сферы, зависимость в оси тела от широты имеет вид:
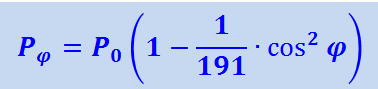 .
.
На полюсе Pφ совпадает с P0; на экваторе Pφ наиболее отличается от P0.
Силы Кориолиса. Покажем, что во вращающейся системе на тело, перемещающееся относительно этой системы, действует кроме центробежной, ещё добавочная сила.
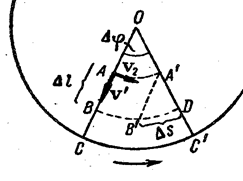
Рассмотри сперва частный случай. Пусть система представляет собою диск, вращающийся с постоянной угловой скоростью ω вокруг вертикальной оси О (рис. 1.28.6) в направлении, указанном стрелкой. Пусть некоторое тело перемещается равномерно из точки А вдоль радиуса ОС со скоростью V' относительно диска. За время Δt тело пройдёт отрезок Δℓ = AB = ν' ⋅ Δt. За это время Δt в неподвижной системе координат радиус ОС, благодаря вращению диска, повернётся на угол Δφ = ω ⋅ Δt, и тело передвинется из А в Д. В неподвижной системе координат тело принимает одновременно участие в двух движениях: в движении относительно диска со скоростью ν' и в движении вместе со вращающимся диском. Линейная скорость вращения диска различна для разных мест диска. Обозначим её значение в точке А через νr. Двигаясь лишь со скоростью νr тело описало бы дугу AA' и пришло бы в точку A'. Двигаясь одновременно со скоростью νr и относительной скоростью ν', тело должно было бы попасть в точку B' (отрезок A'B' ⎮⎮ AB). На самом деле тело переходит в точку Д. Это происходит за счёт того, что линейная скорость вращения νr возрастает по мере удаления тела от центра вращения. Таким образом, относительно неподвижной системы координат тело, двигаясь вдоль радиуса, непрерывно меняет свою скорость: оно движется ускоренно. Величина этого ускорения а может быть определена по тому добавочному пути 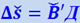 , который тело прошло за время Δt. Из рис. 1.28.6 имеем:
, который тело прошло за время Δt. Из рис. 1.28.6 имеем:
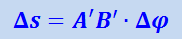 ,
,
или, так как A'B' = Δℓ = ν'Δt и Δφ = ω ⋅ Δt, то
(1.28.4)
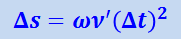 .
.
Рис. 1.28.6 |
Следовательно, добавочный путь Δs возрастает пропорционально квадрату времени Δt. Но пропорциональность пути квадрату времени Δt имеет место при движении с постоянным ускорением α (равномерно-ускоренном движении) при котором
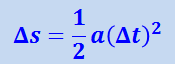 .
.
Сравнивая это выражение с (1.28.4), получим, что тело испытывает ускорение
(1.28.5)
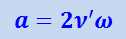 .
.
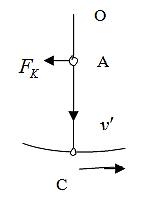
Это ускорение направлено перпендикулярно к относительной скорости ν', и в нашем случае – направо (рис. 1.28.7). Для того, чтобы сообщить телу это ускорение, к нему необходимо приложить силу F, направленную направо и равную F = ma, где m - масса тела. Не будь силы F, тело отклонилось бы во вращающейся вместе с диском системе координат от своего «прямолинейного» движения вдоль радиуса диска.
Рис. 1.28.7 |
Сила FK равная силе F, но направленная в противоположную сторону, будет действовать по третьему закону Ньютона на те связи, которые удерживают тело при его движении на радиусе. Совершенно аналогично, как в ранее рассмотренных случаях ускоренных систем, пользуясь координатной системой, вращающейся вместе с диском, будем считать, что сила FK приложена к самому телу. Таким образом, во вращающейся системе к телу, движущемуся вдоль радиуса со скоростью ν', приложена «инерционная сила»
(1.28.6)
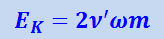 ,
,
направленная перпендикулярно к ν' (в нашем случае налево). Сила FK носит название силы Кориолиса.
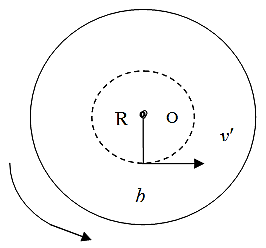
Покажем теперь, что сила Кориолиса существует и в том случае, когда тело движется на диске по окружности с центром на оси вращения (рис. 1.28.8). При движении тела относительно диска со скоростью ν' полная скорость в неподвижной системе координат равна νr + ν' , где νr - линейная скорость вращения диска в том месте, где находится тело. Следовательно, на тело действует центростремительная сила
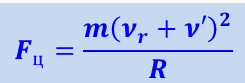 ,
,
где R - расстояние от оси вращения до тела. Возводя в этой формуле сумму в квадрат, получим
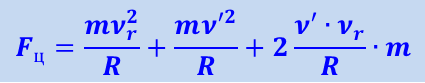 .
.
Рис. 1.28.8 |
В координатной системе, связанной с диском, член 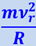 определяет инерционную центробежную силу, вызванную вращением диска с угловой скоростью ω; член
определяет инерционную центробежную силу, вызванную вращением диска с угловой скоростью ω; член 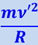 определяет центробежную силу, вызванную относительным движением тела по кругу радиуса R со скоростью ν' ; член
определяет центробежную силу, вызванную относительным движением тела по кругу радиуса R со скоростью ν' ; член
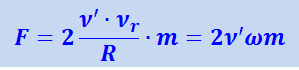
определяет добавочную силу, вызванную одновременным наличием, как вращения диска, так и движения тела относительно диска. Сила FK, равная силе F, но направленная в противоположную сторону, даст для этого случая силу Кориолиса.
Эта сила совпадает по величине с силой, возникающей при движении по радиусу, и направлена также перпендикулярно к относительной скорости.
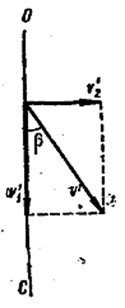
Теперь рассмотрим случай, когда тело движется с относительной скоростью  , направление которой составляет угол β с радиусом ОС (рис. 1.28.9).
, направление которой составляет угол β с радиусом ОС (рис. 1.28.9).
Рис. 1.28.9 |
В этом случае скорость  можно разложить на две составляющие: на составляющую вдоль радиуса ν'1 = ν' ⋅ sinβ и составляющую, перпендикулярную к радиусу, ν'2 = ν' ⋅ sinβ. Составляющей ν'1 по формуле (1.28.6) соответствует кориолисова сила
можно разложить на две составляющие: на составляющую вдоль радиуса ν'1 = ν' ⋅ sinβ и составляющую, перпендикулярную к радиусу, ν'2 = ν' ⋅ sinβ. Составляющей ν'1 по формуле (1.28.6) соответствует кориолисова сила 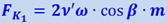 , составляющей ν'2 - сила
, составляющей ν'2 - сила  ; полная сила Кориолиса
; полная сила Кориолиса
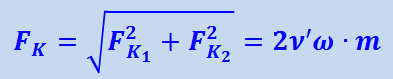 .
.
Таким образом, и для произвольного направления относительной скорости  для силы Кориолиса сохраняется выражение (1.28.6).
для силы Кориолиса сохраняется выражение (1.28.6).
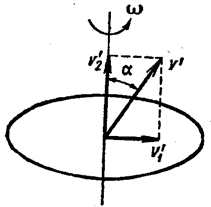
Наконец, рассмотрим самый общий случай, когда тело движется в направлении, составляющем угол α с осью вращения (рис. 1.28.10).
Рис. 1.28.10 |
Разложим скорость  на составляющую
на составляющую 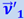 , перпендикулярную к оси вращения, и составляющую
, перпендикулярную к оси вращения, и составляющую 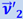 , параллельную оси вращения. Последняя составляющая не обуславливает никакого изменения расстояния от оси и, следовательно, не может вести к появлению добавочных ускорений и сил. Отсюда величина силы Кориолиса определяется лишь составляющей ν'1 = ν' ⋅ sinα. Заменяя в формуле (1.28.6) ν' через ν'1 = ν' ⋅ sinα, получим общее выражение для силы Кориолиса
, параллельную оси вращения. Последняя составляющая не обуславливает никакого изменения расстояния от оси и, следовательно, не может вести к появлению добавочных ускорений и сил. Отсюда величина силы Кориолиса определяется лишь составляющей ν'1 = ν' ⋅ sinα. Заменяя в формуле (1.28.6) ν' через ν'1 = ν' ⋅ sinα, получим общее выражение для силы Кориолиса
(1.28.7)
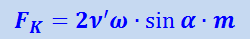
или
(1.28.8)
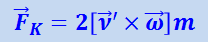 .
.
Направление силы Кориолиса определяется по правилу буравчика.
Как отмечено выше, сила Кориолиса проявляется, в частности, при движениях по поверхности земного шара, обладающего определённой угловой скоростью, благодаря суточному вращению.
Из перечисленных в настоящем разделе эффектов рассмотрим несколько подробнее отклонение плоскости качания маятника.
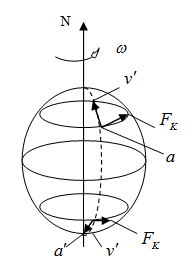
Предположим для простоты, что маятник совершает колебания на северном полюсе. Тогда скорость груза маятника  всё время перпендикулярна к оси земного шара (при большой длине нити) и, следовательно,
всё время перпендикулярна к оси земного шара (при большой длине нити) и, следовательно, 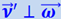 , где
, где  - вектор угловой скорости Земли. В результате на груз маятника действует сила Кориолиса, численно равная FK = 2mν'ω, лежащая в горизонтальной плоскости и направленная вправо по отношению к вектору
- вектор угловой скорости Земли. В результате на груз маятника действует сила Кориолиса, численно равная FK = 2mν'ω, лежащая в горизонтальной плоскости и направленная вправо по отношению к вектору  . Под действием этой силы груз маятника при каждом размахе отклоняется вправо. В результате плоскость качаний маятника будет поворачиваться относительно Земли в направлении часовой стрелки и повернётся на угол 2π за сутки. В случае качаний маятника на широте φ (рис. 1.28.11) плоскость качаний повернётся в сутки на угол 2π ⋅ sinφ.
. Под действием этой силы груз маятника при каждом размахе отклоняется вправо. В результате плоскость качаний маятника будет поворачиваться относительно Земли в направлении часовой стрелки и повернётся на угол 2π за сутки. В случае качаний маятника на широте φ (рис. 1.28.11) плоскость качаний повернётся в сутки на угол 2π ⋅ sinφ.
Рис. 1.28.11 |
Наблюдение отклонения плоскости качаний маятника было впервые проведено Фуко в 1851 г. и послужило прямым доказательством существования суточного вращения Земли.
В заключение обратим ещё раз внимание на то, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчёта.
Для любого из тел, находящихся в неинерциальной системе отсчёта, силы инерции являются внешними, следовательно, здесь нет замкнутых систем. Это означает, что в неинерциальных системах отсчёта не выполняются законы сохранения импульса, энергии и момента импульса.
Возникает вопрос о «реальности» или «фиктивности» сил инерции. В ньютоновской механике, согласно которой сила есть результат взаимодействия тел, на силы инерции можно смотреть как на «фиктивные», «исчезающие» в инерциальных системах отсчёта. Однако возможна и другая их интерпретация. Так как взаимодействия тел осуществляются посредством силовых полей, то силы инерции можно рассматривать как воздействия, которым подвергаются тела со стороны каких-то реальных силовых полей, и тогда их можно считать «реальными». Независимо от того, рассматриваются ли силы инерции в качестве «фиктивных» или «реальных», многие явления, о которых упоминалось в настоящем разделе, объясняются с помощью сил инерции.
к к к