ФИЗИКА
1.5.1. Кинетическая энергия релятивистской частицы
Определим эту величину таким же путём, как и в ньютоновской механике, т.е. как величину, приращение которой равно работе действующей на частицу силы. Сначала найдём приращение кинетической энергии dEK частицы под действием силы 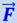 на элементарном пути
на элементарном пути 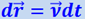 :
:
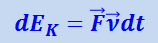 .
.
Согласно (1.23.1)
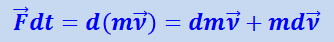 ,
,
где т – релятивистская масса. Подставив этот результат в предыдущее уравнение, получим
(1.24.1)
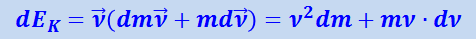 ,
,
где учтено, что 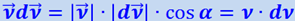 (α - угол между
(α - угол между  и
и 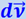 ).
).
Выражение (1.24.1) можно упростить, используя формулу (1.22.2). Возведём (1.22.2) в квадрат и приведём её к виду
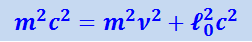 .
.
Найдём дифференциал этого выражения с учётом того, что m0 и c - постоянные величины:
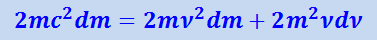
или
(1.24.2)
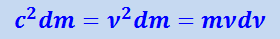 .
.
Сравнив (1.24.1) и (1.24.2), получим
(1.24.3)
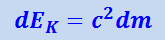 .
.
Таким образом, приращение кинетической энергии частицы пропорционально приращению её релятивистской массы. Кинетическая энергия покоящейся частицы равна нулю, а её масса равна массе покоя m0. Поэтому, проинтегрировав (1.24.3), получим
(1.24.4)
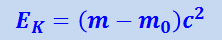
или
(1.24.5)
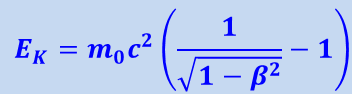 ,
,
где β = V/c. Это и есть выражение для релятивистской кинетической энергии частицы.
Убедимся, что при малых скоростях (β<<1) выражение (1.24.5) переходит в ньютоновское. Для этого воспользуемся формулой бинома Ньютона, согласно которой
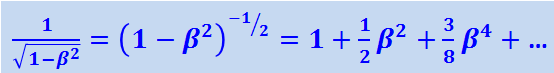 .
.
При β<<1 можно ограничиться первыми двумя членами этого ряда. Тогда
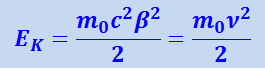 .
.
Таким образом, при больших скоростях кинетическая энергия частицы определяется релятивистской формулой (1.24.5), отличной от m0ν2/2.
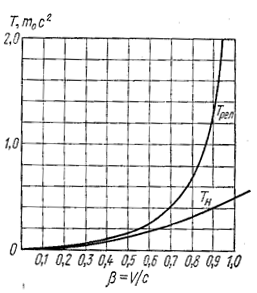
Рис. 1.24.1 |
На рис. 1.24.1 показаны для сравнения графики зависимости от β релятивистской EKp и ньютоновской кинетических энергий. Их различие особенно сильно проявляется в области скоростей, сравнимых со скоростью света.
к к к