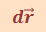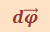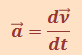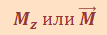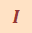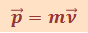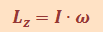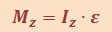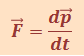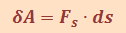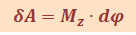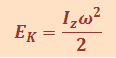ФИЗИКА

1.3.5. Момент импульса. Закон сохранения момента импульса

Момент импульса во вращательном движении является аналогом импульса в поступательном движении. Эта величина вводится в рассмотрение, поскольку в замкнутой системе она сохраняется.

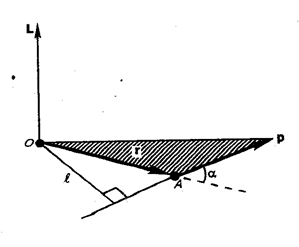
Момент импульса материальной точки. Моментом импульса материальной точки А относительно неподвижной точки О называется величина, определяемая векторным произведением

(1.14.1)

,

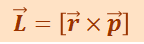где 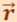- радиус-вектор, проведённый из точки О в точку А;

- импульс материальной точки (рис. 1.14.1).

- аксиальный вектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от 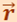к 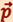(правило правой руки). Модуль вектора момента-импульса

,

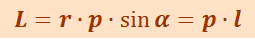где α - угол между векторам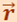и и ;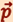

ℓ - плечо вектора 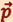относительно точки О.

Моментом импульса относительно неподвижной оси Z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определённого относительно произвольной точки О данной оси. Момент импульса Lz не зависит от положения точки О на оси Z.

Момент импульса твёрдого тела относительно проходящей через него неподвижной оси ОО’. Чтобы найти этот момент мысленно разобьём тело на материальные точки. При этом каждая материальная точка движется по окружности постоянного радиуса ri со скоростью 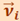. Скорость 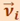и импульс 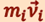перпендикулярны этому радиусу, т.е. радиус является плечом вектора 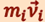. С учётом этого момент импульса отдельной материальной точки равен

(1.14.2)

и направлен по оси вверх ( по правилу правого винта).

Момент импульса твёрдого тела относительно оси ОО’ найдём как сумму моментов импульса составляющих его материальных точек:

.

Учитывая, что νi = ωri , получим

,

т.е.

(1.14.3)

.

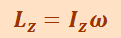Продифференцируем (1.14.3) по времени:

,

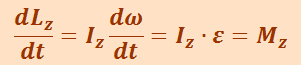т.е.

(1.14.4)

.

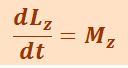Формула (1.14.4) – ещё одна форма уравнения динамики вращательного движения. Можно показать, что выполняется соотношение:

(1.14.5)

,

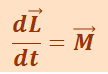где 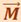- момент внешних сил.

В замкнутой системе 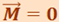и 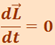, откуда

(14.6)

.

Выражение (1.14.6) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы с течением времени сохраняется.

Закон сохранения момента импульса – фундаментальный закон природы. Он связан с изотропностью пространства. Изотропность пространства означает, что свойства замкнутой физической системы не меняются при повороте системы на заданный угол относительно любой произвольно выбранной оси вращения.

Проявление закона сохранения (1.14.6) мы можем соблюдать, следя за тем, как фигуристка начинает и заканчивает вращение. Фигуристка начинает вращение с раскинутыми в стороны руками и далеко отставленной ногой (большие ri, а значит большой момент инерции). Затем она опускает одну руку и поднимает другую, придвигает ногу и вообще старается вся стать как можно ближе к своей оси вращения. При этом ri для некоторых элементов тела уменьшаются, что приводит к уменьшению её момента инерции, а значит (14.3) к возрастанию ω. И вот в результате вы видите вместо спортсменки только сплошное и длительное мелькание. Чтобы остановиться, фигуристка просто разводит руки в стороны.

В заключение сопоставим основные величины и уравнения, определяющие его поступательное движение и вращение тела вокруг неподвижной оси.

Таблица 1.14.1

Отметим, что приведённые в табл.1.14.1 уравнения для вращательного движения могут быть получены из уравнений для поступательного движения путём замены аналогичных величин. К примеру, кинетическая энергия при вращении может быть получена из формулы кинетической энергии при поступательном движении следующим образом. Аналогом т является I, аналогом ν является ω . Подставляя эти величины в формулу 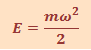, будем иметь .

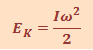к к к