ФИЗИКА

1.3.4. Основное уравнение динамики вращательного движения твёрдого тела

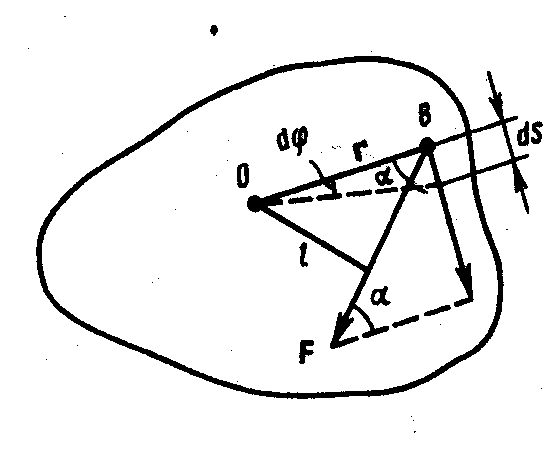
Пусть твёрдое тело вращается вокруг оси перпендикулярной рисунку и проходящей через точку О (рис. 1.13.1)

Пусть сила 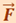приложена в точке В, находящейся от оси на расстоянии r, α - угол между направлением силы и радиусом-вектором 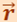. Найдём работу при вращении тела. Так как тело твёрдое, то работа силы 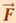равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол dφ точка приложения В проходит путь ds = r ⋅ dφ и работа равна произведению проекции силы на направление смещения на величину смещения:

(1.13.1)

,

т.к. 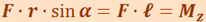- момент силы относительно оси Z.

Работа при вращении тела идёт на увеличение его кинетической энергии 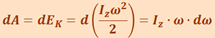, поэтому

(13.2)

.

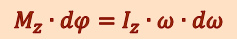Разделим (1.13.2) на или

(1.13.3)

,

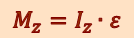где - угловое ускорение.

Уравнение (1.13.3) представляет собой основное уравнение динамики вращательного движения относительно неподвижной оси.

Если ось вращения совпадает с главной осью инерции, то это уравнение пишется в виде: .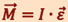

к к к