ФИЗИКА
1.3.2. Кинетическая энергия твёрдого тела при вращении

Пусть твёрдое тело произвольной формы вращается вокруг проходящей через него неподвижной оси ОО’ (рис. 1.11.1). Найдём кинетическую энергию этого тела.
Для этого мысленно разобьём тело на материальные точки с массами m1, m2,..., mi, находящимися на расстоянии r1, r2,..., rn от оси. При вращении твёрдого тела составляющие его материальные точки будут описывать окружности разных радиусов r и будут иметь различные скорости 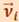 .
.
Кинетическую энергию вращающегося тела найдём как сумму кинетических энергий составляющих его материальных точек:
(1.11.1)
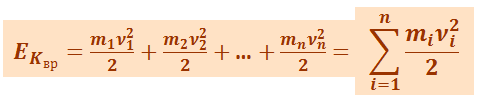
Так как мы рассматриваем абсолютно твёрдое тело, то угловая скорость вращения всех материальных точек одинакова:
(1.11.2)
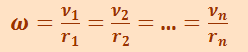 .
.
Рис. 1.11.1 |
Подставив (1.11.2) в (1.11.1), получим:
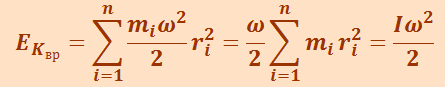 ,
,
где 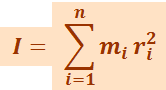 - момент инерции тела относительно оси вращения.
- момент инерции тела относительно оси вращения.
Таким образом, кинетическая энергия вращающегося тела
(1.11.3)
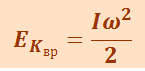 .
.
В случае плоского движения тела (например, цилиндр скатывается с наклонной плоскости без скольжения) энергия движения складывается из энергии поступательного движения и энергии вращения:
(1.11.4)
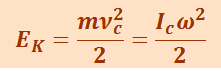 ,
,
где т – масса катящегося тела,
vc – скорость центра масс тела,
Ic – момент инерции тела относительно оси, проходящей через его центр масс,
ω - угловая скорость.
к к к