ФИЗИКА
Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:
(1.10.1)

В случае непрерывного распределения масс эта сумма сводится к интегралу
(1.10.2)
 ,
,
где интегрирование производится по всему объёму V тела (ρ - плотность тела).
В качестве примера найдём момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно оси ОО, проходящей через его центр масс. Мысленно разобьём цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r + dr. Момент инерции каждого полого цилиндра dI=ρr2dν=2πr3hρdr. Тогда момент инерции всего цилиндра равен
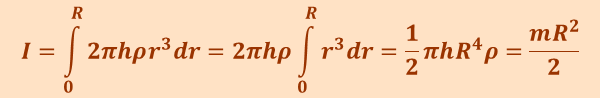 ,
,
так как масса цилиндра равна πR2hρ.
Если известен момент инерции тела относительно оси ОО, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси О’O’ определяется теоремой Штейнера: момент инерции тела I относительно произвольной оси равен моменту его инерции Ic относительно параллельной оси, проходящей через центр масс тела С плюс произведение массы тела т на квадрат расстояния а между осями (рис. 1.10.1):
Рис. 10.1 |
(1.10.3)
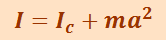 .
.
К настоящему времени моменты инерции тел правильной формы вычислены и приводятся в таблицах.
Момент инерции тела характеризует его инертные свойства при вращении.
к к к
