ФИЗИКА
1.2.7. Закон сохранения энергии
Кинетическая энергия. Пусть материальная точка массы т движется под действием некоторой силы 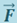 . Найдём работу, которую совершает эта сила на элементарном перемещении
. Найдём работу, которую совершает эта сила на элементарном перемещении 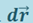
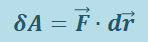 .
.
Учитывая, что 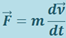 и
и 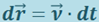 , получим:
, получим:
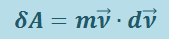 .
.
Скалярное произведение 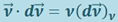 , где:
, где: 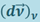 - проекция вектора
- проекция вектора 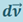 на направление вектора
на направление вектора 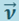 . Как видно из рис. 1.9.1, эта проекция равна dν - приращению модуля вектора скорости. Поэтому
. Как видно из рис. 1.9.1, эта проекция равна dν - приращению модуля вектора скорости. Поэтому 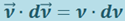 и элементарная работа
и элементарная работа 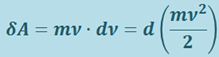 .
.
Рис. 1.9.1 |
Из последнего соотношения видно, что работа результирующей силы 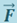 идёт на приращение некоторой величины (стоящей в скобках), которую называют кинетической энергией:
идёт на приращение некоторой величины (стоящей в скобках), которую называют кинетической энергией:
(1.9.1)
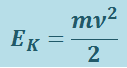 .
.
Таким образом, приращение кинетической энергии материальной точки при элементарном перемещении равно
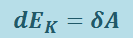 ,
,
а при конечном перемещении из точки 1 в точку 2
(1.9.2)
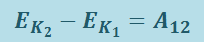 .
.
Отсюда, если A12 > 0, то  , если A12 < 0, то
, если A12 < 0, то  .
.
Кинетическая энергия механической системы – это энергия механического движения этой системы.
Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Силы бывают консервативными и неконсервативными (диссипативными). Консервативные – это такие силы, работа которых не зависит от того, по какой траектории тело перемещается из одного положения в другое, а зависит только от начального и конечного положений. Примером могут служить гравитационные и кулоновские силы.
Неконсервативные – это силы, работа которых зависит от траектории перемещения тела из одной точки в другую (например, силы трения или силы сопротивления).
Поля консервативных сил называются потенциальными. Находясь в таком поле, тело обладает потенциальной энергией Ep. Работа консервативных сил при бесконечно малом изменении конфигурации системы равна приращению потенциальной энергии, взятом со знаком минус, так как работа совершается за счёт убыли потенциальной энергии:
(1.9.3)

или
 ,
,
откуда
(1.9.4)
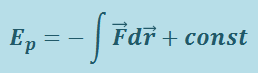 ,
,
т.е. потенциальная энергия определяется с точностью до произвольной постоянной. Работа A12 на конечном перемещении равна
(1.9.5)
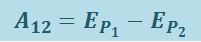 .
.
Обычно потенциальную энергию на поверхности Земли считают равной нулю, а энергию тела в других положениях отсчитывают от этого уровня.
Из (1.9.4) следует:
(1.9.6)
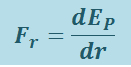 .
.
Поскольку направление 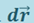 выбрано произвольно, то (1.9.6) выполняется и для других направлений, например, для направлений координатных осей x, y, z
выбрано произвольно, то (1.9.6) выполняется и для других направлений, например, для направлений координатных осей x, y, z
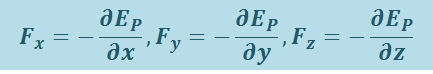 ,
,
или в векторной форме:
(1.9.7)
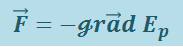 ,
,
где
(1.9.8)
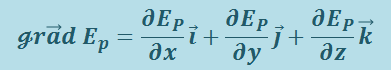 ,
,
(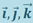 - единичные векторы координатных осей). Вектор, определяемый соотношением (1.9.8), называется градиентом скаляра Ep.
- единичные векторы координатных осей). Вектор, определяемый соотношением (1.9.8), называется градиентом скаляра Ep.
Конкретный вид функции Ep зависит от характера силового поля. Нетрудно показать, что потенциальная энергия тела массой т, поднятого на высоту h над поверхностью Земли, равна
(1.9.9)
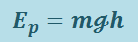 ,
,
где h – отсчитывается от нулевого уровня.
В замкнутой системе полная механическая энергия системы Е остаётся постоянной
(1.9.10)
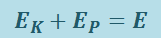 .
.
Выражение (1.9.10) представляет собой закон сохранения механической энергии.
Этот закон связан с однородностью времени. Однородность времени проявляется в том, что физические законы инвариантны относительно выбора начала отсчёта времени. Например, при свободном падении тела в поле сил тяжести его скорость и пройденный путь зависят лишь от начальной скорости и продолжительности свободного падения тела и не зависят от того, когда тело начало падать.
Если в системе действуют также неконсервативные силы (например, силы трения), то полная механическая энергия системы не сохраняется.
Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида. С учётом этой энергии закон сохранения энергии выполняется всегда.
к к к