ФИЗИКА
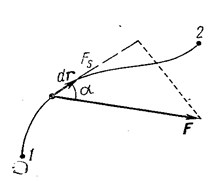
Пусть материальная точка под действием силы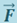 
совершает перемещение по некоторой траектории 1-2 (рис. 1.8.1).
Рис. 1.8.1 |
В общем случае сила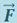 
в процессе движения может меняться как по модулю, так и по направлению. Рассмотрим элементарное перемещение 
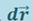, в пределах которого силу 
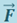можно считать постоянной.
Действие силы на перемещении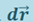 
характеризуют элементарной работой δA силы 
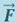на перемещении 
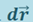. Численно она равна скалярному произведению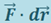 
(1.8.1)
,
где α- угол между векторами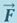 
и 
,
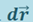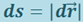- элементарный путь,
Fs - проекция вектора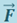 
на вектор 
.
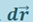Величина δA - алгебраическая: в зависимости от угла между векторам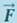и 
и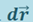 
она может быть как положительной, так и отрицательной, а, в частности, равной нулю (если 
).
Интегрируя (суммируя) выражение (1.8.1) по всем элементарным участкам пути от точки 1 до точки 2, найдём работу силы на данном пути:
(1.8.2)
.
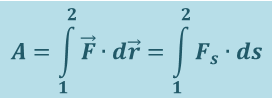Формула (1.8.2) справедлива не только для материальной точки, но и вообще для любого тела (или системы тел). Надо только иметь в виду, что под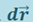 
(или ds) следует понимать перемещение точки приложения силы 
.
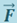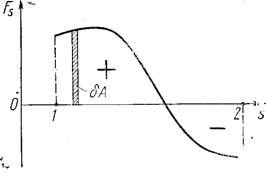
Выражению (1.8.2) можно придать наглядный геометрический смысл. Изобразим график Fs как функцию положения частицы на траектории. Пусть, например, этот график имеет вид, показанный на рис. 1.8.2.
Рис. 1.8.2 |
Из рисунка видно, что элементарная работа δA численно равна заштрихованной полоске, а работа А на пути от точки 1 до точки 2 – площади фигуры, ограниченной кривой, ординатами 1 и 2 и осью s. При этом площадь фигуры над осью s берётся со знаком плюс (она соответствует положительной работе), а площадь фигуры под осью s – со знаком минус (она соответствует отрицательной работе).
Единица работы – джоуль (Дж): 1 Дж - работа, совершаемая силой 1 Н на пути 1 м (1 Дж = 1 Н×м).
Мощность. Для характеристики скорости, с которой совершается работа, вводят величину, называемую мощностью N:
(1.8.3)
,
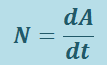т.е. мощность – это работа, совершаемая силой за единицу времени. За время dt сила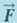 
совершает работу 
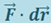. Тогда мощность, развиваемая этой силой в данный момент времени
(1.8.4)
,
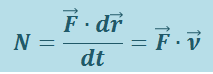где N – величина скалярная.
Единица мощности – ватт (Вт): 1 Вт - мощность, при которой за 1 с совершается работа 1 Дж (1 Вт = 1 Дж/с).
к к к