ФИЗИКА

1.2.5. Уравнение движения тела переменной массы

Движение некоторых тел сопровождается изменением их массы, например масса ракеты, уменьшается вследствие истечения газов, образующихся при сгорании топлива и т.п.

Получим уравнение движения тела переменной массы на примере движения ракеты. Если в момент времени t масса ракеты т, а её скорость , то по истечении времени dt её масса уменьшится на dm и будет равной m - dm, а скорость станет равной . Изменение импульса системы за отрезок времени dt

,

где - скорость истечения газов относительно ракеты.

Тогда (величиной - пренебрегли).

Если на систему действуют внешние силы, то , поэтому

или

(1.7.1)

.

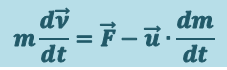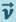Второе слагаемое в (1.7.1) называют реактивной силой . Если противоположен по направлению, то ракета ускоряется, а если совпадает с 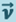, то тормозится.

Таким образом, мы получили уравнение движения тела переменной массы (уравнение И.В. Мещерского)

(1.7.2)

.

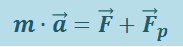Применим (1.7.1) к движению ракеты, на которую не действуют никакие внешние силы. Полагая и считая, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим

,

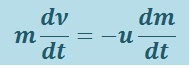откуда

.

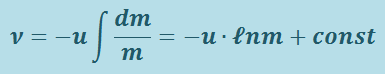Значение const определим из начальных условий. Если в начальный момент времени скорость ракеты равна нулю, а её стартовая масса m0, то const = u ⋅ ℓnm0 . Следовательно,

(1.7.3)

.

Это соотношение называется формулой Циалковского. Она показывает, что:

1) чем больше конечная масса ракеты т, тем больше должна быть стартовая масса ракеты m0;

2) чем больше скорость истечения у газов, тем больше может быть конечная масса при данной стартовой массе ракеты.

к к к