ФИЗИКА
Центром масс системы материальных точек называется точка С, положение которой определяется радиус-вектором
,
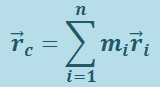где 
и 
- соответственно масса и радиус-вектор i-й материальной точки;
n - число материальных точек в системе;
т - масса всей системы.
Найдём скорость центра масс
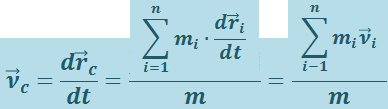
Учитывая, что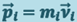 
, а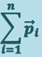 
есть импульс 
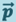системы, получим
(1.6.1)
,
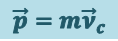т.е. импульс системы равен произведению массы системы на скорость её центра масс. Подставив (1.6.1) в (1.5.1), будем иметь
(1.6.2)
,
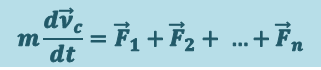т.е. центр масс системы движется так, как если бы вся масса системы была сосредоточена в этой точке и к ней были бы приложены все внешние силы.
Ускорение центра масс совершенно не зависит от точек приложения внешних сил. Если 
, то 
. А если это так, то и импульс системы 
.
Уравнение (1.6.2) по форме совпадает с основным уравнением динамики материальной точки и является его естественным обобщением на систему материальных точек.
к к к