ФИЗИКА
Динамика базируется на законах Ньютона, которые являются результатом обобщения экспериментальных данных.
Первый закон Ньютона: материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения по инерции до тех пор, пока воздействие со стороны других тел не заставит её изменить это состояние.
Во Вселенной практически невозможно найти тело, не испытывающее внешнего воздействия, а, значит, невозможно непосредственно экспериментально подтвердить первый закон Ньютона. Однако с его помощью можно объяснить ряд опытов, что является косвенным подтверждением этого закона. К примеру, монета, лежащая на пластинке плексигласа, закрывающей горлышко бутылки, при резком щелчке по плексигласу в горизонтальной плоскости падает в бутылку, пассажиры автомобиля при резком торможении продолжают движение вперёд и т.д.
Таким образом, из первого закона Ньютона следует, что тело может двигаться как при наличии, так и при отсутствии внешнего воздействия. Следовательно, скорость сама по себе не показывает, действуют на тело внешние силы или нет. Ответ на фундаментальный вопрос, какая физическая величина является однозначным показателем наличия внешнего воздействия, был дан Ньютоном во втором законе.
Второй закон Ньютона. Тело движется прямолинейно и равномерно по абсолютно гладкой поверхности лишь в том случае, когда отсутствует внешнее воздействие. Если подтолкнуть тело в направлении движения, его скорость увеличится. Воздействие на тело в направлении противоположном его движению, уменьшает скорость тела. Следовательно, внешнее воздействие изменяет скорость. Таким образом, не скорость, а ускорение является показателем наличия или отсутствия внешнего воздействия.
Степень воздействия характеризуют силой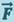 
. Сила векторная величина. В результате действия силы тело приобретает ускорение или изменяет форму и размеры.
Физическая природа взаимодействий может быть различной. Существуют четыре фундаментальных взаимодействия: сильное, электромагнитное, слабое и гравитационное. Силы в механике Ньютона имеют гравитационную и электромагнитную природу. Однако силы различной природы можно измерять в одних и тех же единицах с помощью одних и тех же эталонов.
Связь между ускорением и силой определяется вторым законом Ньютона: произведение массы материальной точки (тела) т на её ускорение равно действующей на него силе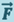 
:
(1.4.1)
.
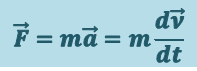Если на тело действует несколько сил, то равнодействующая равна
(1.4.2)
.
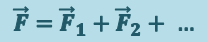Единицей силы в СИ является ньютон (Н). Ньютон – это такая сила, которая сообщает телу массой 1 кг ускорение 1 м/с2.
Масса тела – физическая величина, являющаяся мерой инертности тела. Единицей массы в СИ является кг.
Инертность – физическое свойство, заключающееся в том, что любое тело оказывает сопротивление изменению его скорости (как по модулю, так и по направлению). При прочих равных условиях, чем больше масса тела, тем труднее его сдвинуть.
Отметим, что уравнение (1.4.1) получает конкретное содержание только после того, как установлен вид зависимости силы от определяющих её величин (например, F = -kx , где k – коэффициент упругости).
Учитывая, что масса материальной точки (тела) в классической механике есть величина постоянная, в выражении (1.4.1) её можно внести под знак производной:
(1.4.3)
.
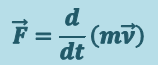Векторная величина
(1.4.4)
,
численно равная произведению массы материальной точки на её скорость и имеющая направление скорости, называется импульсом этой материальной точки.
Подставляя (1.4.4) в (1.4.3), получим
(1.4.5)
.
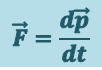Это выражение – более общая формулировка второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на неё силе. Выражение (1.4.5) называется уравнением движения материальной точки.
Третий закон Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:
(1.4.6)
,
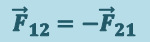где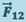 
- сила, действующая на первую материальную точку со стороны второй;
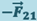- сила, действующая на вторую материальную точку со стороны первой.
Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.
Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам попарного взаимодействия между материальными точками.
В третьем законе Ньютона предполагается, что обе силы равны по модулю в любой момент времени независимо от движения точек. Это утверждение соответствует ньютоновскому представлению о мгновенном распространение взаимодействий – предположению, которое носит название принципа дальнодействия. Согласно этому принципу, взаимодействие между телами распространяется в пространстве с бесконечно большой скоростью.
В действительности это не так – существует конечная максимальная скорость распространения взаимодействий, которая равна скорости света в вакууме. Поэтому третий закон Ньютона (а также и второй) имеет определённые пределы применимости. Однако при скоростях тел, значительно меньших скорости света, с которыми имеет дело ньютоновская механика, оба закона выполняются с очень большой точностью. Свидетельством этому являются хотя бы расчёты траекторий планет и искусственных спутников, которые проводятся с «астрономической» точностью именно с помощью законов Ньютона.
Законы Ньютона выполняются только в инерциальных системах отсчёта.
Земля же движется относительно Солнца и звёзд по криволинейной траектории, имеющей форму эллипса. Криволинейное движение всегда происходит с некоторым ускорением. Кроме того, Земля совершает вращение вокруг своей оси. По этим причинам система отсчёта, связанная с земной поверхностью, движется с ускорением относительно гелиоцентрической системы отсчёта и не является инерциальной. Однако ускорение такой системы настолько мало, что в большом числе случаев её можно считать практически инерциальной. Но иногда неинерциальность системы отсчёта, связанной с Землёй, оказывает существенное влияние на характер рассматриваемых относительно неё механических явлений. Некоторые из таких случаев мы рассмотрим впоследствии.
В соответствии с принципом относительности Галилея законы механики должны быть одинаковыми во всех инерциальных системах отсчёта. Это значит, в частности, что уравнение (1.4.1) будет иметь один и тот же вид в любой инерциальной системе отсчёта. Действительно, масса т материальной точки как таковой не зависит от скорости, т.е. одинакова во всех системах отсчёта. Кроме того, для инерциальных систем отсчёта одинаковым является и ускорение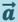 
точки (1.3.5). Сила 
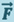тоже не зависит от выбора системы отсчёта, поскольку она определяется только взаимным расположением и скоростью материальной точки относительно окружающих тел, а эти величины, согласно релятивистской кинематики, в разных инерциальных системах отсчёта одинаковы.
Таким образом, все три величины 
и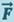 
, входящие в уравнение (4.1), не меняются при переходе от одной инерциальной системы отсчёта к другой, а, следовательно, не меняется и само уравнение (4.1). Другими словами, уравнение 
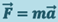инвариантно относительно преобразований Галилея.
Законы Ньютона являются основными законами механики. Они позволяют, по крайней мере, в принципе, решить любую механическую задачу; кроме того, из них могут быть выведены все остальные законы механики.
к к к