ФИЗИКА

1.2.1. Инерциальные системы отсчёта

В кинематике, где речь идёт лишь об описании движений и не затрагивается вопрос о причинах, вызывающих эти движения, никакой принципиальной разницы между различными системами отсчёта нет.

Совершенно иначе дело обстоит в динамике – при изучении законов движения. В принципе можно взять любую из бесчисленного множества систем отсчёта. Однако законы механики в разных системах отсчёта имеют различный вид, и может оказаться, что в произвольной системе отсчёта законы даже совсем простых явлений будут весьма сложными. Естественно возникает задача отыскания такой системы отсчёта, в которой законы механики были бы возможно более простыми.

Для решения этой задачи рассмотрим ускорение материальной точки, относительно некоторой произвольной системы отсчёта. Опыт показывает, что причиной ускорения могут быть как действие на данную точку каких-то определённых тел, так и свойства самой системы отсчёта.

Можно, однако, предположить, что существует такая система отсчёта, в которой ускорение материальной точки целиком обусловлено только взаимодействием с другими телами. Свободная материальная точка, не подверженная действию никаких других тел, движется относительно такой системы отсчёта прямолинейно и равномерно, или, как говорят, по инерции. Такую систему отсчёта называют инерциальной.

Как показали наблюдения над ускорениями планет, инерциальной является гелиоцентрическая система отсчёта. В ней начало координат находится в центре Солнца, а оси проведены в направлении определённых звёзд. В настоящее время инерциальность гелиоцентрической системы отсчёта подтверждается всей совокупностью опытов.

Любая другая система отсчёта, движущаяся равномерно и прямолинейно относительно гелиоцентрической системы, является также инерциальной.

Таким образом, существует не одна, а бесчисленное множество инерциальных систем отсчёта. Системы отсчёта, движущиеся с ускорением относительно инерциальных систем, называются неинерциальными.

Важной особенностью инерциальных систем отсчёта является то, что по отношению к ним пространство и время обладают определёнными свойствами симметрии. А именно: опыт убеждает, что в этих системах отсчёта пространство однородно и изотропно, а время однородно.

Однородность и изотропность пространства заключается в том, что свойства пространства одинаковы в различных точках (однородность), а в каждой точке одинаковы во всех направлениях (изотропность).

Однородность времени заключается в том, что протекание физических явлений (в одних и тех же условиях) в разное время их наблюдения одинаково. Иначе говоря, различные моменты времени эквивалентны друг другу по своим физическим свойствам.

Отметим, что по отношению к неинерциальным системам отсчёта пространство является неоднородным и неизотропным. Время в этих системах отсчёта также является неоднородным, т.е. его различные моменты будут не эквивалентны друг другу.

Принцип относительности Галилея. Для инерциальных систем отсчёта справедлив принцип относительности, согласно которому все инерциальные системы по своим механическим свойствам эквивалентны друг другу. Это значит, что никакими механическими опытами, проводимыми «внутри» данной инерциальной системы, нельзя установить покоится эта система или движется. Во всех инерциальных системах отсчёта свойства пространства и времени одинаковы, одинаковы также и все законы механики. Данное утверждение составляет содержание принципа относительности Галилея.

Вышесказанное свидетельствует об исключительности свойств инерциальных систем отсчёта, в силу которых именно эти системы должны, как правило, использоваться при изучении механических явлений.

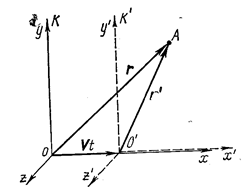
Преобразования Галилея. Найдём формулы преобразования координат при переходе от одной инерциальной системы отсчёта к другой. Пусть инерциальная система К’ движется со скоростью 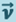относительно другой инерциальной системы К. Выберем оси координат x', y', z' К’-системы параллельно соответствующим осям x, y, z К-системы так, чтобы оси x' и x совпадали между собой и были направлены вдоль вектора (рис. 1.3.1). Взяв за начало отсчёта времени момент, когда начала координат О’ и О совпадали,

запишем соотношение между радиусами-векторами и 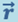одной и той же точки А в К’ и К-системах:

(1.3.1)

и, кроме того

(1.3.2)

.

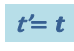Соотношения (1.3.1) и (1.3.2) представляют собой преобразования Галилея. В координатах эти преобразования имеют вид:

(1.3.3)

.

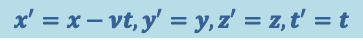Продифференцировав (1.3.1) по времени, найдём классический закон преобразования скорости точки при переходе одной инерциальной системы отсчёта к другой:

(1.3.4)

.

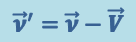Дифференцируя (1.3.4) по времени, получим

(1.3.5)

,

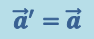т.е. ускорение точки одинаково во всех инерциальных системах отсчёта.

к к к