ФИЗИКА
1.1.2. Кинематика твёрдого тела
Различают пять видов движения твёрдого тела. При этом основными являются поступательное движение и вращение вокруг неподвижной оси. Остальные могут быть получены как суперпозиция этих движений.
Поступательное движение. Это такое движение твёрдого тела, при котором любая прямая, связанная с телом, всё время остаётся параллельной своему начальному положению. Например, машина, едущая по прямому участку пути; кабина колеса обозрения и т.д.
При поступательном движении все точки твёрдого тела совершают за один и тот же промежуток времени равные перемещения. Поэтому скорости и ускорения всех точек в данный момент времени одинаковы. Это позволяет свести изучение поступательного движения твёрдого тела к изучению движения отдельной точки тела, т.е. к задаче кинематики точки.
Таким образом, поступательное движение твёрдого тела может быть полностью описано, если известны зависимость от времени радиуса-вектора любой точки этого тела, положение и его скорость в начальный момент времени.
Вращение вокруг неподвижной оси. Пусть твёрдое тело вращается вокруг неподвижной оси OO'. Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения.
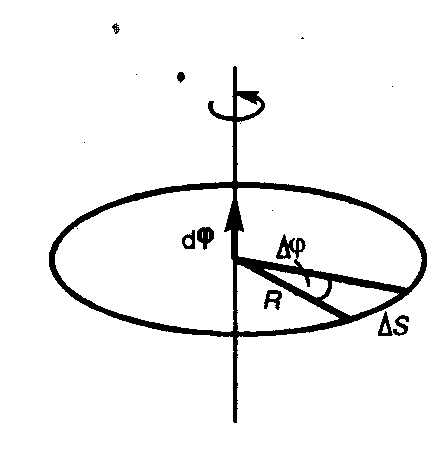
Изменение положения тела за время dt можно характеризовать углом поворота некоторой точки А, движущейся по окружности радиуса R (рис. 1.2.1).
Рис. 1.2.1 |
Угол поворота принято характеризовать вектором  , модуль которого равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта.
, модуль которого равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта.
Векторы, направления которых определяются направлением вращения, называются псевдовекторами или аксиальными векторами. Эти векторы не имеют определённых точек приложения: они могут откладываться из любой точки оси вращения.  - аксиальный вектор. Так же аксиальными являются векторы угловой скорости
- аксиальный вектор. Так же аксиальными являются векторы угловой скорости 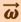 и углового ускорения
и углового ускорения 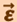 .
.
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
(1.2.1)
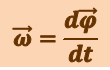
Вектор 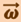 направлен так же, как вектор
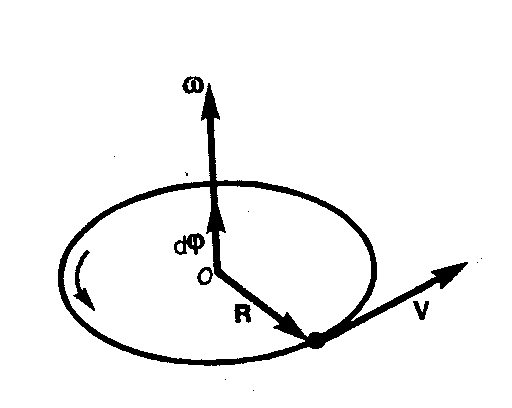
направлен так же, как вектор  , вдоль оси вращения по правилу правого винта (рис. 1.2.2). Размерность угловой скорости
, вдоль оси вращения по правилу правого винта (рис. 1.2.2). Размерность угловой скорости  , где Т – время, а её единица – радиан в секунду (рад/с). Из рис. 1.2.2 следует, что линейная скорость точки
, где Т – время, а её единица – радиан в секунду (рад/с). Из рис. 1.2.2 следует, что линейная скорость точки
Рис. 1.2.2 |
(1.2.2)
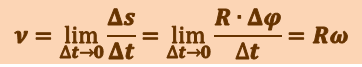 .
.
Более строго (1.2.2) нужно записать как векторное произведение:
(1.2.3)
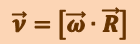 .
.
При этом модуль векторного произведения, по определению, равен 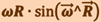 , а направление совпадает с направлением поступательного движения правого винта при его вращении от
, а направление совпадает с направлением поступательного движения правого винта при его вращении от 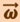 к
к 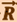 .
.
Если ![]() , то вращение равномерное и его можно характеризовать периодом вращения Т-временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2π. Так как промежутку времени ∆t = T соответствует ∆φ = 2π, то
, то вращение равномерное и его можно характеризовать периодом вращения Т-временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2π. Так как промежутку времени ∆t = T соответствует ∆φ = 2π, то
 .
.
Число полных оборотов, совершаемых телом при равномерном его движении по окружности в единицу времени, называется частотой вращения:
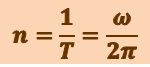 ,
,
откуда
(1.2.4)

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
(1.2.5)
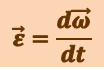 .
.
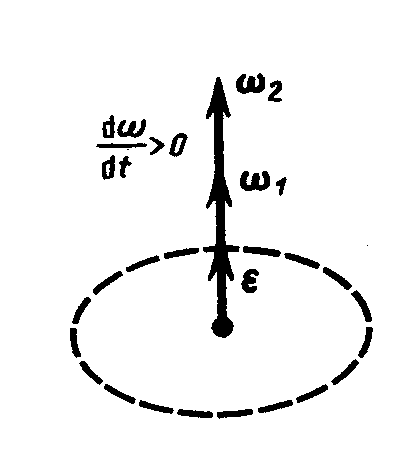
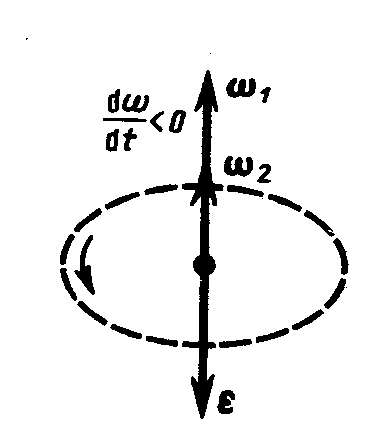
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения. Причём при ускоренном движении 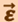 сонаправлен вектору
сонаправлен вектору 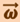 (рис. 1.2.3а), при замедленном – противоположен ему (рис. 1.2.3б).
(рис. 1.2.3а), при замедленном – противоположен ему (рис. 1.2.3б).
а) |
б) |
Рис. 1.2.3 |
|
Установим связь между полным ускорением а некоторой точки вращающегося тела и угловыми величинами. Для этого продифференцируем (1.2.3) по времени:
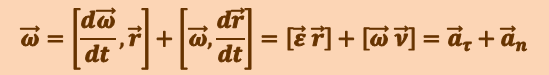 .
.
Здесь:
(1.2.6)
 .
.
Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение ατ, нормальное ускорение αn) и угловыми величинами (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами:
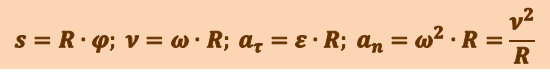 .
.
В случае равнопеременного движения по окружности ( )
)
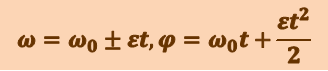 ,
,
где ω0 - начальная угловая скорость.
к к к