ФИЗИКА
3.7.4. Ток при замыкании и размыкании цепи
По правилу Ленца дополнительные токи, возникающие вследствие самоиндукции, всегда направлены так, чтобы противодействовать изменениям тока в цепи. Это приводит к тому, что установление тока при замыкании цепи и убывание тока при размыкании цепи происходит не мгновенно, а постепенно.
Найдём сначала характер изменения тока при размыкании цепи. Пусть в цепь с не зависящей от I индуктивностью L и сопротивлением R включён источник э.д.с. ε (рис. 3.7.4). В цепи буде течь постоянный ток:
(3.7.13)

Рис. 3.7.4 |
(сопротивление источника тока считаем пренебрежимо малым).
В момент времени t = 0 отключим источник тока, замкнув одновременно цепь накоротко переключателем П. Как только сила тока в цепи начнёт убывать, возникнет э.д.с. самоиндукции, противодействующая этому убыванию:
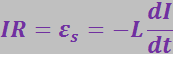
или
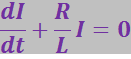
Разделив переменные, получим:

Отсюда
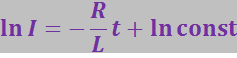
Потенцирование даёт:
(3.7.14)

Значение const найдём из начальных условий. При t = 0 I = I0. Отсюда
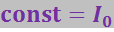
Подставив это значение в (3.7.14), будем иметь:
(3.7.15)
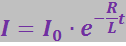
Итак, после отключения источника сила тока в цепи убывает по экспоненциальному закону (кривая 1 на рис. 3.7.5). Скорость убывания определяется величиной:
(3.7.16)
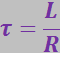
называемой постоянной времени цепи. Подставив (3.7.16) в (3.7.15), получим:
(3.7.17)
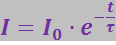
Рис. 3.7.5 |
Из (3.7.17) τ – время, в течение которого сила тока уменьшается в е раз. Если просто разорвать цепь с большой индуктивностью, возникающее высокое индукционное напряжение создаёт искуру или дугу в месте разрыва.
Теперь рассмотрим случай замыкания цепи. После подключения источника (рис. 3.7.4), до тех пор пока сила тока не достигнет установившегося значения (3.7.13), в цепи кроме э.д.с. ε будет действовать э.д.с. самоиндукции. Следовательно, в соответствии с законом Ома:
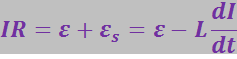
или
(3.7.18)
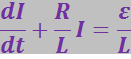
Из теории дифференциальных уравнений известно, что общее решение линейного неоднородного уравнения можно получить, прибавив любое его частное решение к общему решению соответствующего однородного уравнения. Общее решение однородного уравнения имеет вид (3.7.14). Легко убедиться в том, что ![]() является частным решением (3.7.18). Следовательно, общим решением уравнения (3.7.18) будет функция:
является частным решением (3.7.18). Следовательно, общим решением уравнения (3.7.18) будет функция:

В начальный момент сила тока I равна нулю. Отсюда ![]() . Таким образом,
. Таким образом,
(3.7.19)
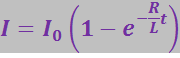
Эта функция описывает нарастание тока в цепи после подключения к ней источника э.д.с. График функции (3.7.19) дан на рис. 3.7.5 (кривая 2).
к к к