ФИЗИКА

3.6.2. Напряжённость магнитного поля

Напишем выражение для циркуляции поля (3.6.1):

(3.6.4)

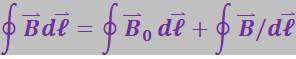
Согласно (3.5.45):

(3.6.5)

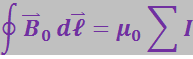
где – алгебраическая сумма макроскопических токов, охватываемых контуром, по которому производится интегрирование, т.е. алгебраическая сумма токов, текущих через произвольную поверхность S, ограниченную контуром.

Для поля , создаваемого молекулярными токами, должно выполняться аналогичнон соотношение:

(3.6.6)

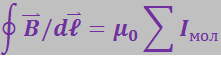
где – алгебраическая сумма молекулярных токов, текущих через поверхность S.

Подставим (3.6.5) и (3.6.6) в (3.6.4):

(3.6.7)

Здесь мы сталкиваемся с затруднением: чтобы найти циркуляцию поля , нужно знать сумму молекулярных токов, которая в свою очередь зависит от .

Способ, позволяющий обойти это затруднение, аналогичен способу, которым мы воспользовались в п. 3.2.3. Оказывается можно найти такую вспомогательную величину

(3.6.8)

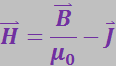
циркуляция которой по некоторому контуру равна алгебраической сумме макроскопических токов, охватываемых этим контуром:

(3.6.9)

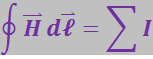
Эту величину называют напряжённостью магнитного поля. Её единицей измерения является ампер на метр (A/м). Напряжённость магнитного поля является аналогом электрического смещения .

Установим связь между напряжённостью магнитного поля и индукцией. При этом будем полагать, что в каждой точке магнетика

(3.6.10)

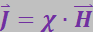
где χ - безразмерная величина, называемая магнитной восприимчивостью.

Подставив (3.6.10) в (3.6.8), получим:

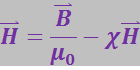
откуда

(3.6.11)

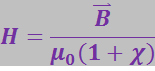
Безразмерная величина

(3.6.12)

называется относительной магнитной проницаемостью или просто магнитной проницаемостью вещества. Она может быть как больше, так и меньше единицы.

С учётом (3.6.12) формуле (3.6.11) можно придать вид:

(3.6.13)

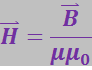
Таким образом, напряжённость магнитного поля есть вектор, имеющий то же направление, что и вектор , но в раз меньший по модулю (в анизотропных средах векторы и не совпадают по направлению).

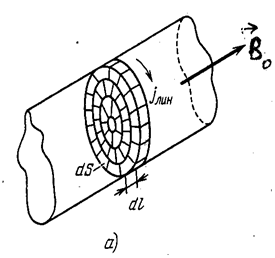
Выясним физический смысл магнитной проницаемости. Допустим, что имеется однородное магнитное поле в вакууме, которое мы будем характеризовать с помощью либо вектора , либо вектора . Внесём в это поле (внешнее) бесконечно длинный круглый стержень из однородного и изотропного материала и расположим его вдоль линий (рис. 3.6.1). Под действием поля молекулярные токи установятся так, что их магнитные моменты расположатся вдоль оси стержня, а плоскости токов станут перпендикулярными к этой оси.

Рассмотрим молекулярные токи, лежащие в одном из поперечных сечений стержня. В любой точке внутри стержня соседние молекулярные токи текут в противоположных направлениях, так что их совместное действие равно нулю. Нескомпенсированными будут лишь участки токов, примыкающие к поверхности стержня. Таким образом, суммарное действие молекулярных токов будет таким, какое вызвал бы макроскопический ток, текущий по поверхности стержня перпендикулярно к его оси. Обозначим линейную плотность этого тока через . Согласно (3.5.46) цилиндр, обтекаемый током, эквивалентен соленоиду с числом ампер-витков , равным . Магнитная индукция внутри такого соленоида определяется формулой (3.5.48). Следовательно, магнитная индукция дополнительного поля, создаваемого молекулярными токами внутри стержня, равна:

(5.6.14)

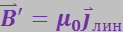
В соответствии с правилом правого винта направление совпадает с направлением (см. рис. 3.6.1). Вне стержня равно нулю.

Выделим мысленно в стержне перпендикулярный к его оси слой толщины (рис. 3.6.1). Молекулярные токи, расположенные в этом слое, эквивалентны круговому току силы . Согласно формуле (5.30) магнитный момент этого тока равен:

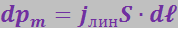
где S – площадь поперечного сечения стержня.

Разделив на объём слоя , получим намагниченность стержня:

(3.6.15)

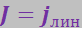
Таким образом, модуль намагниченности стержня равен линейной плотности обтекающего стержень молекулярного тока.

С учётом (3.6.15) формула (3.6.14) принимает вид:

(3.6.16)

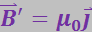
Сложив векторы и , найдём магнитную индукцию внутри стержня:

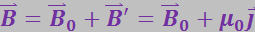
Подстановка этого выражения в формулу (3.6.8) даёт напряжённость поля внутри стержня:

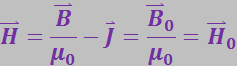
Следовательно, напряжённость поля в стержне совпадает с напряжённостью внешнего поля.

Умножив на , получим магнитную индукцию внутри стержня:

(3.6.17)

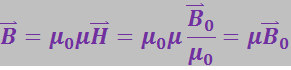
Отсюда следует, что магнитная проницаемость μ показывает, во сколько раз усиливается поле в магнетике.

к к к